Part2 EDA and Base Model
Shimpei Ikeno, Satyaki Roy, Yuta Suzuki, and Takeru Sone
2022-07-12
In Part I…
We introduced our approach to building a practical multivariate time series forecasting model. We introduced the data set from a past Kaggle Competition and created a seasonal naive model which will be our baseline. In part II, we will kick off the next topic of Feature engineering.
Time Series Feature Engineering
Welcome to our Data Science Blog! I am Satyaki, a data scientist in the Time Series Forecasting Practice Team at Nomura Research Institute, Ltd.
In part II of 時系列予測、Kaggle、データサイエンス実践、series, we will focus on feature engineering, specifically those used to train ML models on time series.
Compared to traditional time series models such as ARIMA or Exponential smoothing, Machine learning models are trained on cross-sectional data, meaning each training example is assumed to be an independent sample from a distribution. Thus the performance of ML time series forecast models depends heavily on the quality of features provided and the proper cross-validation techniques used.
Let us look at our data again. We have a time series for sales for each store-dept combination.
## # A tibble: 6 x 5
## Store Dept Date Weekly_Sales IsHoliday
## <dbl> <dbl> <date> <dbl> <lgl>
## 1 1 1 2010-02-05 24924. FALSE
## 2 1 1 2010-02-12 46039. TRUE
## 3 1 1 2010-02-19 41596. FALSE
## 4 1 1 2010-02-26 19404. FALSE
## 5 1 1 2010-03-05 21828. FALSE
## 6 1 1 2010-03-12 21043. FALSEJust from the date column, we will show how to create multiple time series features, as listed below.
## [1] "Date" "IsHoliday" "Year"
## [4] "Month" "Week" "Dayofyear"
## [7] "Is_month_end" "Is_month_start" "Is_quarter_end"
## [10] "Is_quarter_start" "Is_year_end" "Is_year_start"
## [13] "weekday_cos" "weekday_sin" "day_month_cos"
## [16] "day_month_sin" "month_year_cos" "month_year_sin"
## [19] "day_year_cos" "day_year_sin" "quarter"
## [22] "weekNumber" "AfterIsHoliday" "BeforeIsHoliday"
## [25] "AfterIsHoliday_roll" "BeforeIsHoliday_roll" "SuperBowlWeek"
## [28] "LaborDayWeek" "TranksgivingWeek" "ChristmasWeek"
## [31] "AfterSuperBowlWeek" "BeforeSuperBowlWeek" "AfterLaborDayWeek"
## [34] "BeforeLaborDayWeek" "AfterTranksgivingWeek" "BeforeTranksgivingWeek"
## [37] "AfterChristmasWeek" "BeforeChristmasWeek"As you can see above, we can create 37-time series features using the Date and isHoliday columns alone. Additionally, we will create more features with mean/standard deviation encoding.
Let us go into detail on these features, and the other features used in our model:
- Time series features generated by us :
- 1.a. Time lags - To capture the Autoregressive part.
- 1.b. Rolling means - To capture time series trends.
- 1.c. Date features - Features such as month, quarter, Week number, etc. to capture multiple seasonalities.
- 1.d. Holiday features - Features that capture holidays and days to/from holidays.
- 1.e. Mean encoding features - Exogenous features (provided by the competition)
1. Time series features
1.a. Time lags
Most time series data such as sales data have some temporal dependencies in them. The sales of today will depend on yesterday or the same day last week or last month. Thus, Autoregressive features are one of the key features of time series and we will show how we determined which lags to include in our model.


The First plot shows the patterns in sales that occur yearly. This is confirmed by the ACF plot which shows spikes at lags 7,8 and lags 51-53. The ACF plot is used to determine the correlation between lags in a time series. Since our forecast horizon is 39 weeks and our model is a non-recursive ML model, we will use only lags 39 to 53. Even though you can use a larger range of lags, using larger lag values as features can introduce more NA values so we need to be careful. In our case, we chose to use only up to lag 53.
1.b. Rolling means
The trend component of a time series represents a persistent, long-term change in the mean of the series. To see what kind of trend a time series might have, we can use a moving average plot. To compute a moving average of a time series, we compute the average of the values within a sliding window of some defined width. Each point on the graph represents the average of all the values in the series that fall within the window on the left side. The idea is to smooth out any short-term fluctuations in the series so that only long-term changes remain.

As you can see from the above figure, the long-term changes are captured without short-term fluctuations. Along with the moving average features, we also added moving sd of multiple windows to capture the changes in values within the period.

1.c. Date features
Date features, along with lags, provide additional seasonal information to the model. We included multiple seasonal features into our model and let me model choose the best features through regularization.
- Features such as month, quarter, week number, etc. were important features to capture the multiple seasonal patterns in the data.


- Cyclic feature encoding Time series features such as weeks, months, or seasons are cyclic in nature, and thus we try to find a way to preserve their cyclical significance. Each ordinal time feature is transformed into 2 features that together encode equivalent information in a non-monotonic way, and more importantly without any jump between the first and the last value of the periodic range.
The below visualization shows how the movement of the clock can be encoded as a trigonometric curve. Similarly, we will create such curves for days of the month, days of the year, etc.
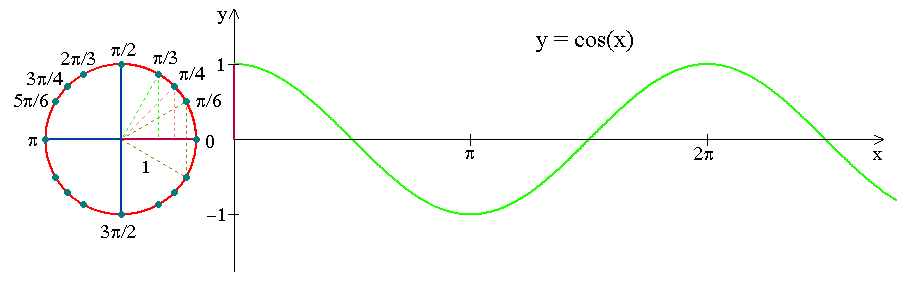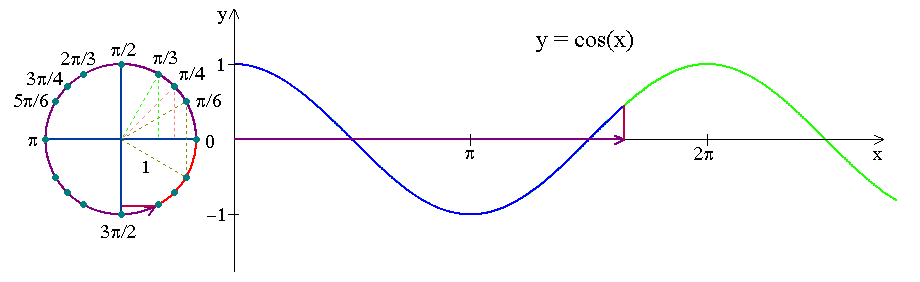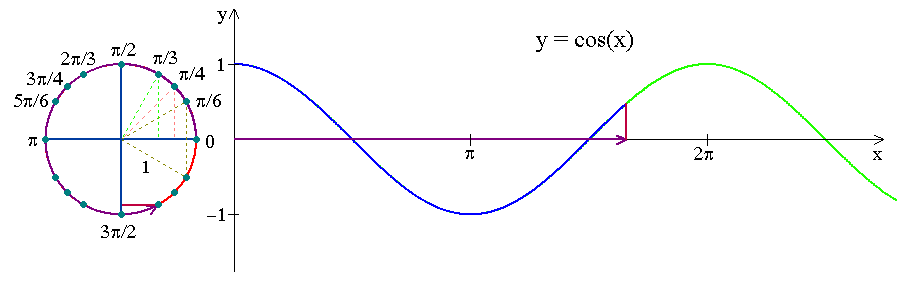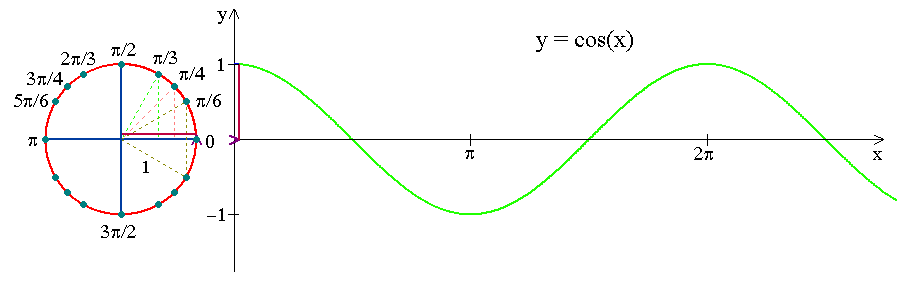
The below sin and cos curves capture the cyclic nature of the day of the month:


The below sin and cos curve captures the cyclic nature of the day of the year and thus has a larger wavelength.


1.d. Holiday Features
Holidays are a very important factor in the competition as the evaluation metric provides 5 times more weight to forecast error on holidays compared to on other days. Furthermore, we found high spikes in sales during Christmas and Thanksgiving, so the model needs to forecast these spikes.
Walmart runs several promotional markdown events throughout the year which precede prominent holidays, the four largest of which are the Super Bowl, Labor Day, Thanksgiving, and Christmas. The below dates were provided by the competition:
- Super Bowl: 12-Feb-10, 11-Feb-11, 10-Feb-12, 8-Feb-13
- Labor Day: 10-Sep-10, 9-Sep-11, 7-Sep-12, 6-Sep-13
- Thanksgiving: 26-Nov-10, 25-Nov-11, 23-Nov-12, 29-Nov-13
- Christmas: 31-Dec-10, 30-Dec-11, 28-Dec-12, 27-Dec-13
The below plots show the features of holidays

As you can imagine, the effect of holidays on sales is not only on those specific days but also on a few days before as people usually shop for gifts before Christmas and Thanksgiving. So, we created the below two features i.e Days after and before holidays to capture these trends.


We are also interested in having multiple holidays in the coming weeks, or the weeks before can impact the sales of a particular week. So, we created the below features.


Multiple ways of encoding the holiday effect as shown above can provide significant performance improvement as it did in our case.
1.e. Mean Encoding
Mean encoding is the process of replacing each distinct value of categorical value with an average value of the target variable we’re trying to predict. As you can guess, this process can lead to overfitting, especially in the time series case since we should not use future data to create target encodings for past predictions. Thus, it is imperative to use time series cross-validation to train the model using mean encoding.

The above diagram illustrates the series of training and test sets, where the blue observations form the training sets, and the orange observations form the test sets. We calculated the mean/sd encodings on the training sets and used in future test sets and thus tuned our hyperparameters using multiple train/test sets in this fashion. We created 36 groups of means and standard deviation encoding features for our ML model.
Below are some of the groups used:
- Store and Dept
- Store, Dept and Holiday
- Store, Dept and Month
- Dept and Christmas week
…..
This is how we provide a baseline mean of sales of each store and dept to the global ML model.

The above figure shows that even for the same dept such as Dep.75, different stores can have very different mean sales.
Thus these encodings can provide multiple baseline features to our global multivariate time series model.
2. Exogenous features
For the competition, we were provided a features.csv with the following features -
- Store - the store number
- Date - the week
- Temperature - the average temperature in the region
- Fuel_Price - the cost of fuel in the region
- MarkDown1-5 - anonymized data related to promotional markdowns that Walmart is running. MarkDown data is only available after Nov 2011 and is not available for all stores all the time. Any missing value is marked with an NA.
- CPI - the consumer price index
- Unemployment - the unemployment rate
- IsHoliday - whether the week is a special holiday week
Also, as mentioned above we had information on the type of holidays such as Christmas, Thanksgiving, etc.
However, the variables from the features.csv data did not provide much value to the model, but we chose to keep them anyway.
As we have shown here, feature engineering can be a key factor in the performance of the model. Many times, such as in this case, the exogenous features available to us do not contribute a lot to model accuracy, thus we need to put our efforts into an exhaustive feature engineering process to capture all the trends and patterns in the time series data. With this data, we were able to create dozens of time series features with only a Date and Holiday column.
Up Next in Part III …
Before going into Machine Learning techniques, we will first look at traditional statistical time series models. We will explain how we used Seasonal ARIMA, Exponential smoothing, TBATS, etc. to create forecasts comparable to or even sometimes better than that of state-of-the-art ML models. See you again in the next blog!
